بایگانی دی ۱۳۹۱

نوح ِ کربلا ...

حتَّی إِذا جَاء أَمْرُنَا وَفارَ التّنور
قحطی آب که باشد؛ خون می جوشد از تنور !
اینجا طوفان ِ سفینة الله ِ کربلاست ...

ولیُ الله که باشی؛ غیرة الله هم هستی!
بر روی نی امّا؛
با چشم بسته قرآن می خواند ...

سه حرف بیش تر نیست؛
مکشوف ترین روضه ی باز ِ کربلا،
الشّــــام
الشّــــام
الشّــــام

...

۱۸ دی ۹۱ ، ۱۹:۲۴

۲

۰ ۰ نظر

ریاضیات تنها زبانی است که پدیده های طبیعی جهان هستی را به خوبی توضیح می دهد. ریاضیات حتی پدیده های اجتماعی _خواه اجتماعات بشری، خواه اجتماعات حیوانی_ را نیز می تواند به خوبی تشریح کند و با ترسیم مدلی برای آنها تغییرات آتی آنها را پیش بینی کند. لوباچفسکی (۱) می گوید؛ هیچ شاخه ای از علم ریاضی _هر اندازه هم که انتزاعی و مجرد باشد_ وجود ندارد که یک روز کاربردی برای آن در توضیح پدیده های دنیای واقعی پیدا نشود.

از کهکشان ها و حرکت سیارات عظیم به دور خورشید ها گرفته تا حرکت ابر ها، بادها، گردبادها و از پرواز فضا پیما های غول پیکر و هواپیماهای عظیم الجثه و حرکت قطارها، کشتی ها و اتومبیل ها گرفته تا افتادن سیبی از درخت و سقوط قطرات باران و حدوث رنگین کمان و حرکت بی امان و خستگی ناپذیر الکترون ها به دور هسته اتم ها و فعل و انفعالات شیمیایی که میلیون ها از آن هر لحظه در طبیعت رخ می دهد و هر گونه تغییر در هر چیز و هر زمان، همه و همه با کمک مدل ها و معادلات ریاضی قابل بررسی هستند. قسمت عمده فیزیک با زبان ریاضی قابل تشریح و فهم است. تئوری کوانتوم و تئوری نسبیت با زبان ریاضی است که کوشش دارند قوانین کائنات را تشریح کرده و توضیح دهند.

گالیله می گوید؛ جهان هستی همواره در برابر دیدگان حیرت زده انسان گسترده خواهد ماند و انسان هرگز نمی تواند آن را درک کند مگر اینکه زبانی را که این جهان با آن نوشته و توضیح داده شده است یاد بگیرد و حروف آن را بشناسد. این زبان چیزی جز ریاضیات نیست و این حروف جز مثلث، دایره و سایر اشکال هندسی چیز دیگری نیستند. بدون این زبان انسان حتی یک کلمه از جهان هستی را نخواهد فهمید و همواره گمشده ای را ماند که در کوچه های پر پیچ و خم سرگردان است.

بسیاری از مردم فکر می کنند که فارغ التحصیل رشته ریاضی فقط کارآیی و کفایت در تدریس ریاضیات را دارد و بس در حالی که امروزه در غرب، بسیاری از کارفرما ها منجمله دولت ها برای استخدام در بخش های مختلف سازمان ها و نهاد های خود علاقه مندند متخصصینی را که استخدام می کنند، دارای پشتوانه خوبی از ریاضیات نیز باشند و به ویژه قادر به تجزیه و تحلیل مسائل موجود در آن کار و مطابقت دادن آنها با مدل های ریاضی و بالاخره حل مسئله باشند.

اینها برخی از دلایلی بودند که آموختن ریاضیات را در عصر امروز ضروری می کنند. اما آموختن ریاضیات یک دلیل دیگر هم دارد و آن این است که برای بسیاری از انسان ها ریاضیات از جذابیت خاصی برخوردار است و آن پی بردن به شگفتی ها و اسرار و زیبایی هایی است که این دانش در ذات خود نهفته دارد.عین حال کاربردی هستن، پیشنهاد میکنم امتحانشون کنید.

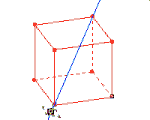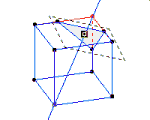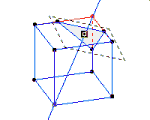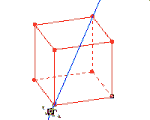
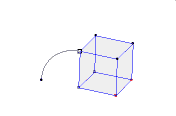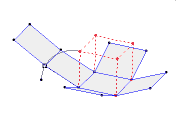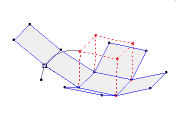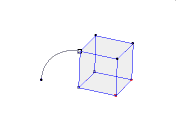
معمولاً تصور و تصویرسازی ذهنی و درک اجسام سه بعدی برای دانش آموزانی که هندسه می خوانند مشکل و سخت است. بنابراین استفاده از رایانه و نرم افزرهای شبیه سازی مانند نرم افزار Calques 3D که در فرانسه طراحی شده است کمک بزرگی برای تصویرسازی ذهنی این اجسام خواهد بود.

کارهایی که میتونید با این نرم افزار انجام بدید

...

۱۱ دی ۹۱ ، ۰۰:۳۱

۲

۰ ۰ نظر

سخنی با خدا به زبان ریاضی

خدایا!
شکر که تو را حدی برایت متصور نیست.
سپاس تو را که بی نهایت مهربانی و بی شمار پاک.
خدایا! حمد و سپاس از آن توست که محیطی بر تمام عالم و تو تکیه گاهی بر تمام موجودات. خداوندا! بنده ای هستم سراپا تقصیر که وجودم بر محور حیات در محاصره پیکانهای شیاطین است.
خدایا! دستم را بگیر که من کسری ازتوأم و وجودم ازآن توست و همه مرا به نام تو می شناسند که من مشتقی از حد بی انتهای توام.
پروردگارا! ببخشای مرا آن لحظه که من بر عمودی غیراز تو تکیه میکنم و همه ستون ها ناپایدارند وقتی تو نباشی.
بارالها! نمی خواهم فقط محیط زندگی ام از نام و یاد تو پر شود که من طالب آنم که مساحت وجودم از تو پر شود.
معبودا! تو آن قدر گویایی که من از وصف تو ناتوانم بند بند وجودم از شعاع نور توست که گرم و روشن می شود. من می خواهم به تو برسم بدون آن که لحظه ای بیم تقسیم و تردید داشته باشم.
بارالها! قلبم از فرآورده هایی انباشته شده که گاه تراکمی از نادرست هاست.
خدایا! من چون مثلثی هستم که می خواهم زاویه کارهایم قاﺋﻢ به وتری باشد که نام تو بر تارک آن نقش بسته باشد.
خدایا ! می خواهم از ۱۰۰ درصد زندگی تو آن را پر کنی وقتی تقسیم می کنند تو باشی وقتی جمع می شوم تو شوی و آن گاه که مرا ضرب می کنند حاصل آن تو یعنی بی نهایت باشی اما مباد آن لحظه که منهای تو باشم.
خداوندا! آن روز را برسان که روح و جسم در تقارن هم و در موازی دستورات تو باشد.
بارالها! در روز معاد ترازوی اعمال مرا آن سان کن که کفه خوبی هایش ولو به ذره ای سنگین تر از اعمال ناشایستم باشد.
پروردگارا! مرا کمک کن، قلبم و جانم آن قدر وسیع شود که هکتار هکتار آن را بذر دوستی بکارم و مهربانی درو کنم.
خداوندا! تمام اعمال نیکم را به توان (n) برسان و آنها را هدیه می کنم به مساحت ۸+۶ تنی که گل وجودم از آنها سرشته شده است.
خدایا مرا ببخشای و در دایره زندگی مرا حیران خودت کن!

...

۱۱ دی ۹۱ ، ۰۰:۲۰

۱

۰ ۰ نظر

نکات المپیادی

1- قواعد موجود در اعداد تواندار :

a ^m× a ⁿ= a ^m+n

مثال

5⁷= ⁴⁺³ 5 = 5⁴× 5³

a ^m÷ a ⁿ= a ^m-n

مثال

² 12 = ^5-7 12 = 12⁵÷12⁷

توضیح

توان صفر : اگر توان عددی برابر صفر باشد ، آن عدد برابر یک است .

( a ^m) ⁿ= a ^mn

مثال

5⁶ = ^3×2 5^{=
3(}5^{2
)}

توضیح

می دانیم 5×5 = 5² بنابراین :

5⁶= 5 × 5× 5 × 5 ×5 ×5 = ³(5×5) = ³(5²)

2- عبارت (a^m)ⁿ با a^mn فرق دارند. (به نقش پرانتز در عبارت اول دقت کنید.)

3- عدد طبیعی n را مجذور کامل گویند هر گاه پس از تجزیه n به عوامل اول توان هر یک از عامل ها زوج باشد .

مثال Å عدد 144 را در نظر بگیرید و آن را به عوامل اول تجزیه کنید . (تقسیم به عوامل اول)

با توجه به اینکه 2و4 عدد زوج هستند ، بنابراین عدد 144 مجذور کامل است .

4- عدد طبیعی n را مکعب کامل گویند هر گاه پس از تجزیه ی n به عوامل اول توان هریک از عوامل ها مضرب 3 باشد .

مثال Å عدد 1728 را در نظر بگیرید و آنرا به عوامل اول تجزیه کنید .

با توجه به اینکه 3 و6 مضرب 3 می باشند ، بنابراین عدد 1728 مکعب کامل است .

عدد 144 را می توان مساحت مربعی به ضلع 12 در نظر گرفت .

می توان نوشت 12=

عدد 144 را مجذور کامل می گویند .

عدد 1728 را می توان حجم مکعبی به ضلع 12 در نظر گرفت .

1728 = 12×12×12 = 12³= حجم مکعب

می توان نوشت : 1728 = 12³ و عدد 1728 را مکعب کامل گویند .

5- اگر یکان عددی 0، 1، 5، 6 باشد ، آن عدد را به توان هر عدد طبیعی برسانیم ، یکان عدد حاصل با یکان عدد اولیه برابر است

مثال Å

یکان های 10 و 10000 هر دو صفر می باشد. ۱۰^۴ = ۱۰×۱۰×۱۰× ۱۰ = ۱۰۰۰۰

یکان های 11 و 1331 هر دو یک می باشد . 1331 = 11×11×11 = 11³

یکان های 15 و 3375 هر دو 5 می باشد . 3375 = 15×15×15 = 15³

یکان های 16 و 256 هر دو 6 می باشد . 256 = 16×16 = 16²

...

۰۸ دی ۹۱ ، ۱۷:۲۸

۱

۰ ۰ نظر

نمونه سوال

1.

اگر زیر رادیکال جمع یا تفریق داشته باشیم ، نمی توانیم از تک تک جملات جذر بگیریم بلکه باید حاصل جمع یا تفریق را به دست آورده سپس جذر بگیریم.

2. جذرگیری از راه تجزیه: می خواهیم جذر عددی را از راه تجزیه محاسبه کنیم، ابتدا عدد را به حاصل ضرب عوامل اول تجزیه می کنیم. سپس از حاصل ضرب آن عوامل جذر می گیریم.

اگر نمای عددی زوج باشد، کافی است پایه را نوشته و نمای آن را نصف کنیم.

مثال: